Graphene hv scan

Simple workflow for analyzing a photon energy scan data of graphene as simulated from a third nearest neighbor tight binding model. The same workflow can be applied to any photon energy scan.

Import the “fundamental” python libraries for a generic data analysis:

import numpy as np
import matplotlib.pyplot as plt

Instead of loading the file as for example:

# from navarp.utils import navfile
# file_name = r"nxarpes_simulated_cone.nxs"
# entry = navfile.load(file_name)

Here we build the simulated graphene signal with a dedicated function defined just for this purpose:

from navarp.extras.simulation import get_tbgraphene_hv

entry = get_tbgraphene_hv(
    scans=np.arange(90, 150, 2),
    angles=np.linspace(-7, 7, 300),
    ebins=np.linspace(-3.3, 0.4, 450),
    tht_an=-18,
)

Plot a single analyzer image at scan = 90

First I have to extract the isoscan from the entry, so I use the isoscan method of entry:

iso0 = entry.isoscan(scan=90)

Then to plot it using the ‘show’ method of the extracted iso0:

iso0.show(yname='ekin')

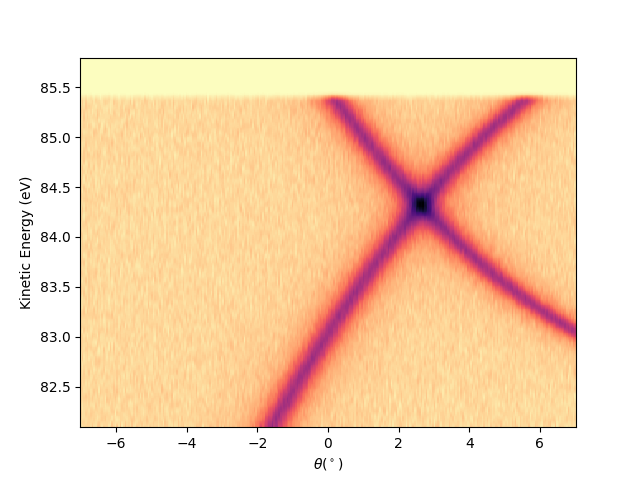
<matplotlib.collections.QuadMesh object at 0x78b8ea88ca90>

Or by string concatenation, directly as:

entry.isoscan(scan=90).show(yname='ekin')

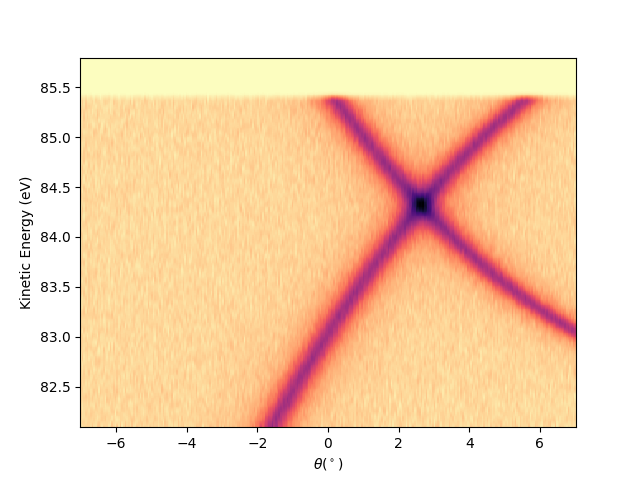
<matplotlib.collections.QuadMesh object at 0x78b8ea946dd0>

Fermi level determination

The initial guess for the binding energy is: ebins = ekins - (hv - work_fun). However, the better way is to proper set the Fermi level first and then derives everything form it. In this case the Fermi level kinetic energy is changing along the scan since it is a photon energy scan. So to set the Fermi level I have to give an array of values corresponding to each photon energy. By definition I can give:

efermis = entry.hv - entry.analyzer.work_fun
entry.set_efermi(efermis)

Or I can use a method for its detection, but in this case, it is important to give a proper energy range for each photon energy. For example for each photon a good range is within 0.4 eV around the photon energy minus the analyzer work function:

energy_range = (
    (entry.hv[:, None] - entry.analyzer.work_fun) +
    np.array([-0.4, 0.4])[None, :])

entry.autoset_efermi(energy_range=energy_range)

scan(eV)  efermi(eV)  FWHM(meV)  new hv(eV)
90.0000  85.3995  59.4  89.9995
92.0000  87.4002  58.9  92.0002
94.0000  89.4002  58.2  94.0002
96.0000  91.4004  58.5  96.0004
98.0000  93.4005  58.4  98.0005
100.0000  95.4003  58.5  100.0003
102.0000  97.4004  58.2  102.0004
104.0000  99.4003  59.1  104.0003
106.0000  101.4004  57.7  106.0004
108.0000  103.4007  57.8  108.0007
110.0000  105.4002  58.5  110.0002
112.0000  107.3998  59.5  111.9998
114.0000  109.4001  58.6  114.0001
116.0000  111.4005  57.8  116.0005
118.0000  113.4004  58.5  118.0004
120.0000  115.4009  57.7  120.0009
122.0000  117.4002  58.9  122.0002
124.0000  119.4003  58.1  124.0003
126.0000  121.4005  58.2  126.0005
128.0000  123.3998  59.2  127.9998
130.0000  125.4005  58.3  130.0005
132.0000  127.4004  58.4  132.0004
134.0000  129.4006  58.2  134.0006
136.0000  131.4005  57.7  136.0005
138.0000  133.4008  59.5  138.0008
140.0000  135.4007  57.1  140.0007
142.0000  137.3999  59.0  141.9999
144.0000  139.4001  59.9  144.0001
146.0000  141.3996  60.5  145.9996
148.0000  143.4001  59.2  148.0001

In both cases the binding energy and the photon energy will be updated consistently. Note that the work function depends on the beamline or laboratory. If not specified is 4.5 eV.

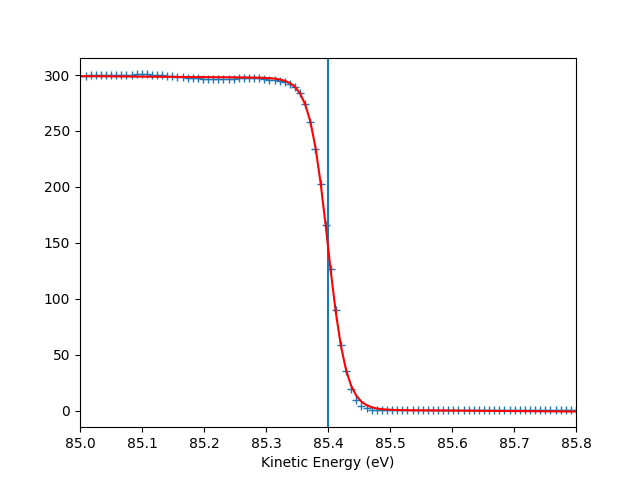
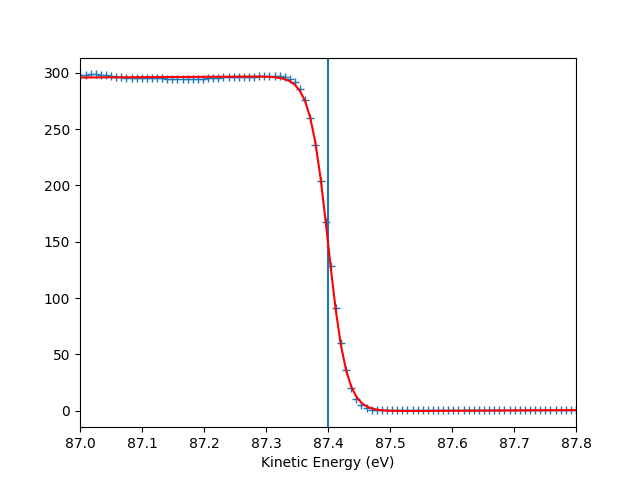
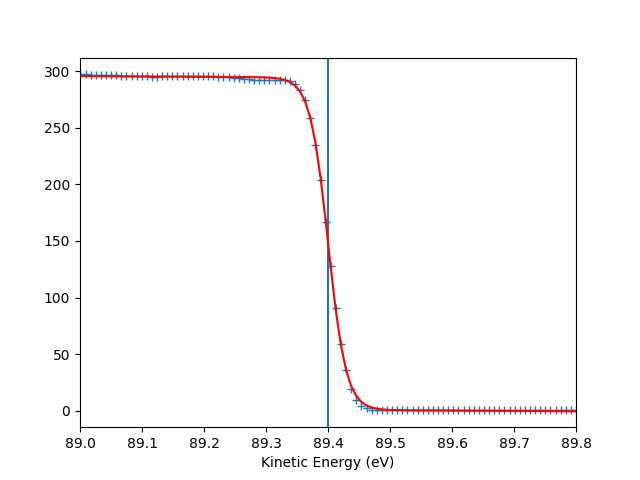
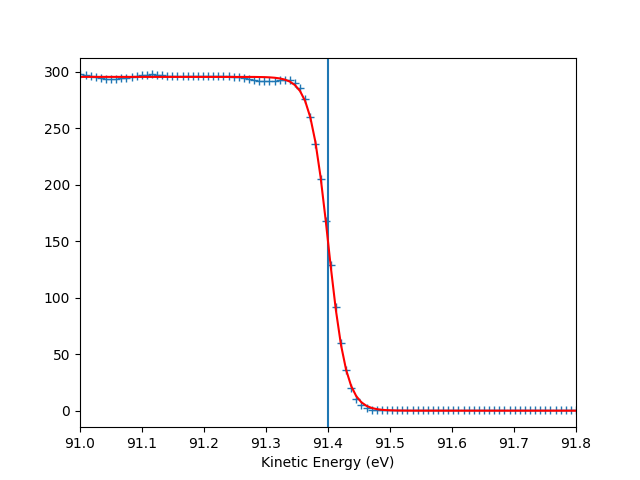
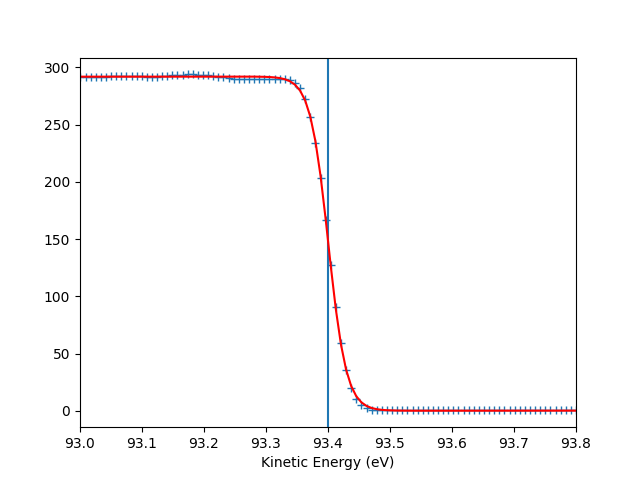
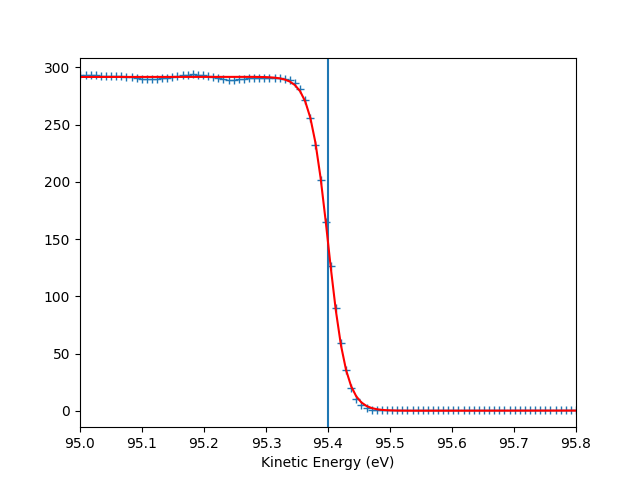
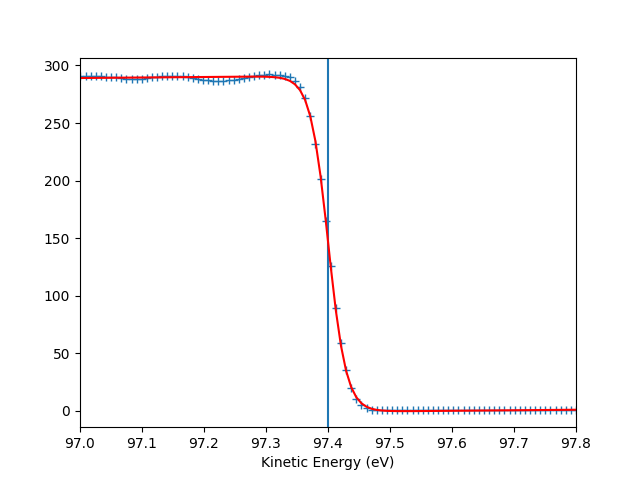
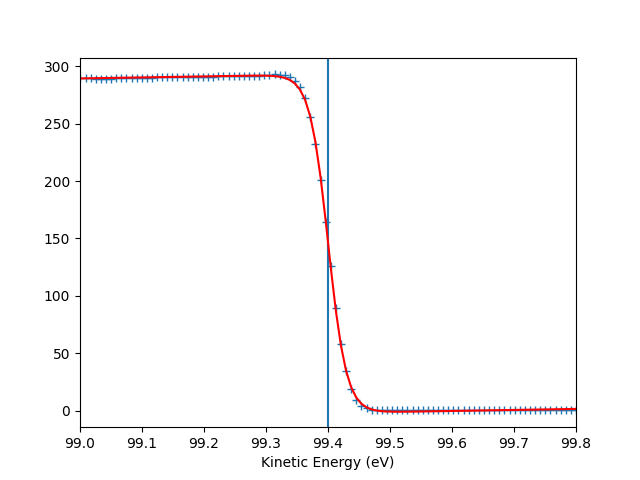
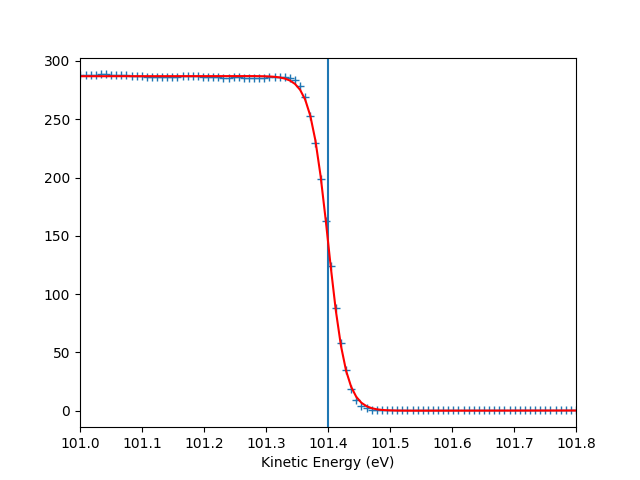
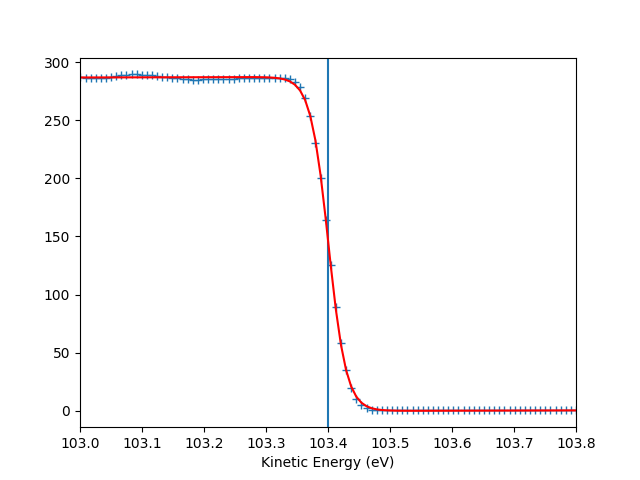
To check the Fermi level detection I can have a look on each photon energy. Here I show only the first 10 photon energies:

for scan_i in range(10):
    print("hv = {} eV,  E_F = {:.0f} eV,  Res = {:.0f} meV".format(
        entry.hv[scan_i],
        entry.efermi[scan_i],
        entry.efermi_fwhm[scan_i]*1000
    ))
    entry.plt_efermi_fit(scan_i=scan_i)

• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

hv = 89.99952201750287 eV,  E_F = 85 eV,  Res = 59 meV
hv = 92.0001973948537 eV,  E_F = 87 eV,  Res = 59 meV
hv = 94.00020032410666 eV,  E_F = 89 eV,  Res = 58 meV
hv = 96.00041349960748 eV,  E_F = 91 eV,  Res = 58 meV
hv = 98.00053087039018 eV,  E_F = 93 eV,  Res = 58 meV
hv = 100.000260514306 eV,  E_F = 95 eV,  Res = 59 meV
hv = 102.00044025669692 eV,  E_F = 97 eV,  Res = 58 meV
hv = 104.0002712950043 eV,  E_F = 99 eV,  Res = 59 meV
hv = 106.00036106751848 eV,  E_F = 101 eV,  Res = 58 meV
hv = 108.00067351202694 eV,  E_F = 103 eV,  Res = 58 meV

Plot a single analyzer image at scan = 110 with the Fermi level aligned

entry.isoscan(scan=110).show(yname='eef')

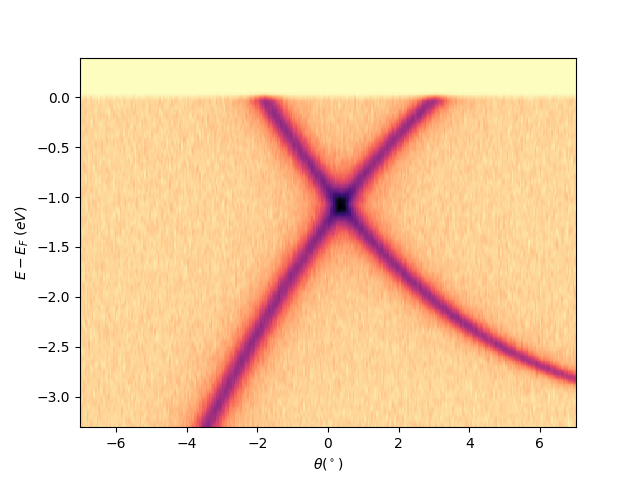
<matplotlib.collections.QuadMesh object at 0x78b8ea2b8e80>

Plotting iso-energetic cut at ekin = efermi

entry.isoenergy(0).show()

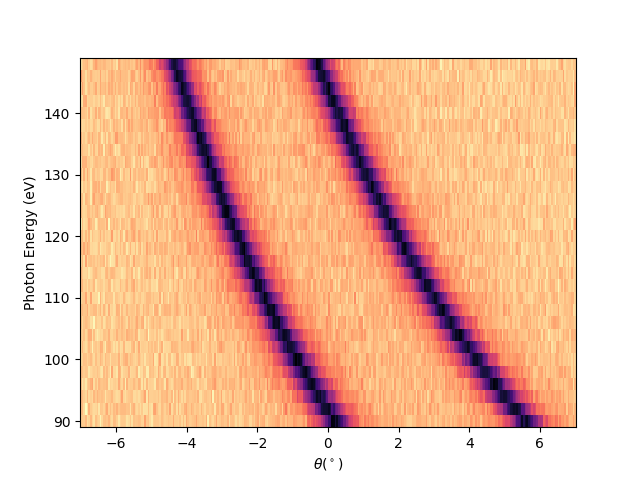
<matplotlib.collections.QuadMesh object at 0x78b8ea345180>

Plotting in the reciprocal space (k-space)

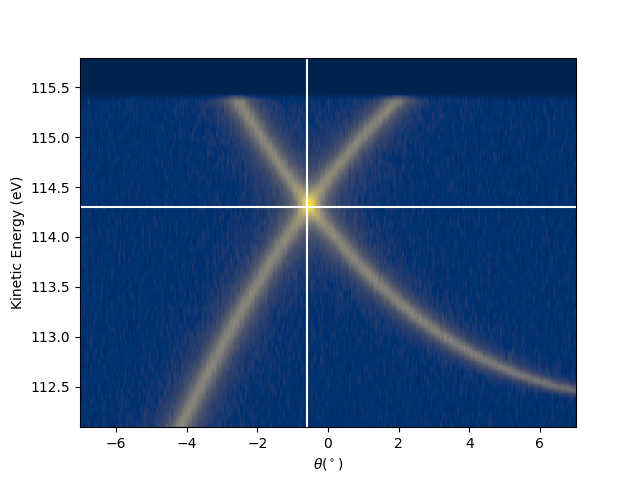
I have to define first the reference point to be used for the transformation. Meaning a point in the angular space which I know it correspond to a particular point in the k-space. In this case the graphene Dirac-point is for hv = 120 is at ekin = 114.3 eV and tht_p = -0.6 (see the figure below), which in the k-space has to correspond to kx = 1.7.

hv_p = 120

entry.isoscan(scan=hv_p, dscan=0).show(yname='ekin', cmap='cividis')

tht_p = -0.6
e_kin_p = 114.3
plt.axvline(tht_p, color='w')
plt.axhline(e_kin_p, color='w')

entry.set_kspace(
    tht_p=tht_p,
    k_along_slit_p=1.7,
    scan_p=0,
    ks_p=0,
    e_kin_p=e_kin_p,
    inn_pot=14,
    p_hv=True,
    hv_p=hv_p,
)

tht_an = -18.040
scan_type =  hv
inn_pot = 14.000
phi_an = 0.000
k_perp_slit_for_kz = 0.000
kspace transformation ready

Once it is set, all the isoscan or iscoenergy extracted from the entry will now get their proper k-space scales:

entry.isoscan(120).show()

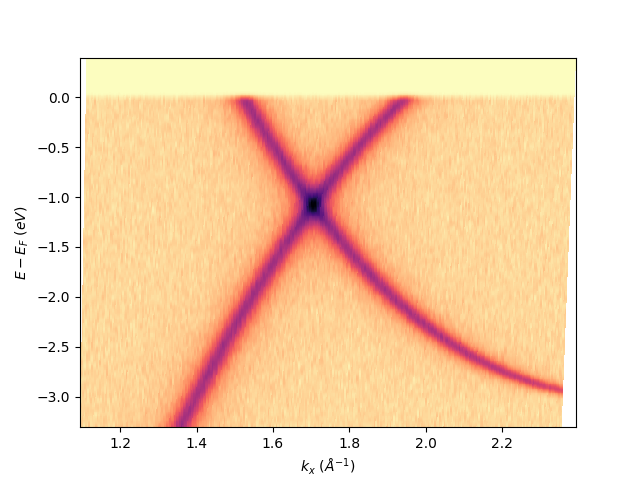
<matplotlib.collections.QuadMesh object at 0x78b8ea0ff490>

sphinx_gallery_thumbnail_number = 17

entry.isoenergy(0).show(cmap='cividis')

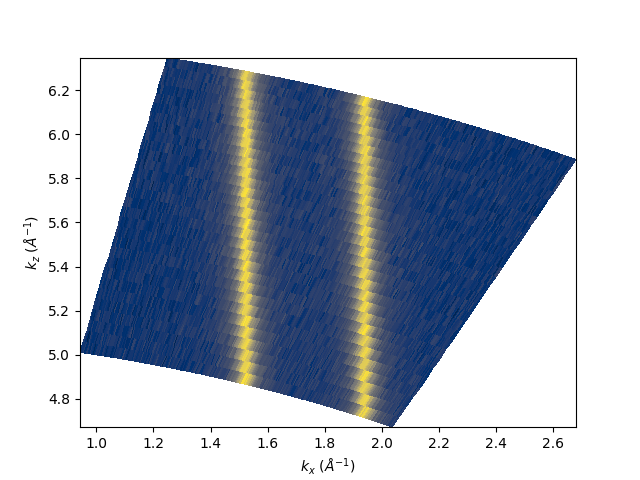
<matplotlib.collections.QuadMesh object at 0x78b8e9f8e050>

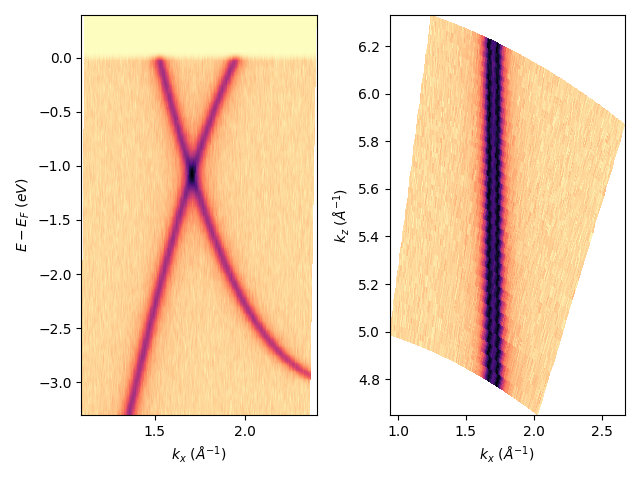
I can also place together in a single figure different images:

fig, axs = plt.subplots(1, 2)

entry.isoscan(120).show(ax=axs[0])
entry.isoenergy(-0.9).show(ax=axs[1])

plt.tight_layout()

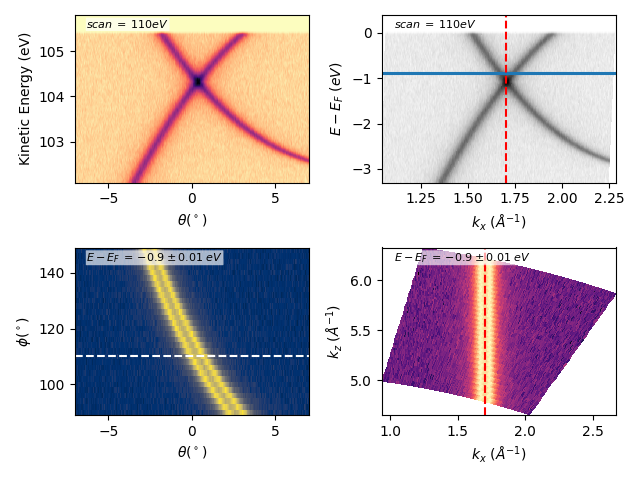
Many other options:

fig, axs = plt.subplots(2, 2)

scan = 110
dscan = 0
ebin = -0.9
debin = 0.01

entry.isoscan(scan, dscan).show(ax=axs[0][0], xname='tht', yname='ekin')
entry.isoscan(scan, dscan).show(ax=axs[0][1], cmap='binary')

axs[0][1].axhline(ebin-debin)
axs[0][1].axhline(ebin+debin)

entry.isoenergy(ebin, debin).show(
    ax=axs[1][0], xname='tht', yname='phi', cmap='cividis')
entry.isoenergy(ebin, debin).show(
    ax=axs[1][1], cmap='magma', cmapscale='log')

axs[1][0].axhline(scan, color='w', ls='--')
axs[0][1].axvline(1.7, color='r', ls='--')
axs[1][1].axvline(1.7, color='r', ls='--')

x_note = 0.05
y_note = 0.98

for ax in axs[0][:]:
    ax.annotate(
        "$scan \: = \: {} eV$".format(scan, dscan),
        (x_note, y_note),
        xycoords='axes fraction',
        size=8, rotation=0, ha="left", va="top",
        bbox=dict(
            boxstyle="round", fc='w', alpha=0.65, edgecolor='None', pad=0.05
        )
    )

for ax in axs[1][:]:
    ax.annotate(
        "$E-E_F \: = \: {} \pm {} \; eV$".format(ebin, debin),
        (x_note, y_note),
        xycoords='axes fraction',
        size=8, rotation=0, ha="left", va="top",
        bbox=dict(
            boxstyle="round", fc='w', alpha=0.65, edgecolor='None', pad=0.05
        )
    )

plt.tight_layout()